EL día 7 de Mayo se realizará el examen de recuperación de matrices.
En esta semana hemos dados posiciones relativas de dos rectas, puede darse unos de estos casos:
-Coincide misma dirección un punto común.
-Son paralelas misma dirección, ningún punto en común.
-Se cortan distinta dirección, un punto común.
-Se cruzan distinta dirección, ningún punto común.
Hemos de aprender a identificar en cual de los cuatro casos estamos partiendo de las expresiones analítica de la recta, es decir, conociendo sus vectores, posiciones, dirección.
Estudio de las posiciones relativas de rectas mediante rango.
-Las rectas coinciden: ran(M)=ran(M')=1
-Las rectas son paralelas: ran(M)=1, ran(M')=2
-Las rectas se cortan: ran(M)=ran(M')=2
-Las rectas se cruzan: ran(M)=2, ran(M')=3
Posiciones relativas de planos y rectas.
El estudio de las posiciones relativas de planos entre sí y de planos y rectas se reducen en todos sus casos, a la resolución de sistemas de ecuaciones. Si embargo, es conveniente prestar atención especial a algunos de ellos.
Dos planos.
Dos planos pueden cortarse, ser paralelos o coincidir. El sistema formado por sus ecuaciones,,
|ax + by + cz + d = 0
|a'x + b'y + c'z + d' = 0
El estudio de sus rango nos da información sobre sus soluciones (es decir, sobre los puntos comunes a ambos planos) y, por tanto, sobre su posición relativa.
miércoles, 24 de abril de 2013
miércoles, 17 de abril de 2013
17 de Abril.
Hemos empezado nuevo tema llamado "Puntos, rectas y planos en el espacio", que en el examen irá unido al anterior.
Simétrico de un punto respecto de otro.
Si A' es el simétrico de A respecto de M, entonces M es el punto medio del segmento AA'. Por ello se verificará la igualdad.
Ejemplo: Calcula el simétrico de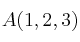
respecto de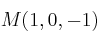 
Llamamos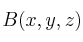
al simétrico buscado. 
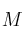será el punto medio del segmento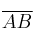 
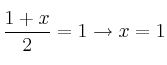
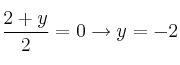
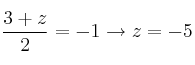
Por tanto, el simétrico es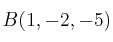
Los ejercicios que hemos realizado en clase son el 1, 2 y 3 pág 156.
Ecuaciones de la recta.
Simétrico de un punto respecto de otro.
Si A' es el simétrico de A respecto de M, entonces M es el punto medio del segmento AA'. Por ello se verificará la igualdad.
Ejemplo: Calcula el simétrico de
respecto de Llamamos
al simétrico buscado. será el punto medio del segmento
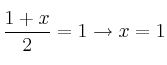
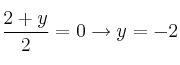
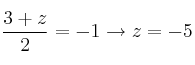
Por tanto, el simétrico es
Los ejercicios que hemos realizado en clase son el 1, 2 y 3 pág 156.
Ecuaciones de la recta.
Ecuación vectorial de la recta
Definimos una recta r como el conjunto de los puntos del espacio, alineados con un punto P y con una dirección dada 
.
.
Si P(x1, y1) es un punto de la recta r, el vector 
tiene igual dirección que , luego es igual a multiplicado por un escalar:
tiene igual dirección que , luego es igual a multiplicado por un escalar:Ecuaciones paramétricas de la recta
Si operamos en la ecuación vectorial de la recta llegamos a la igualdad:
Para que se verifique esta igualdad, se deben cumplir:
Ecuaciones continuas de la recta
Despejando e igualando λ en las ecuaciones paramétricas se tiene:
Ecuaciones implícitas de la recta
Una recta puede venir determinada por la intersección de los planos.
Si en las ecuaciones continuas de la recta quitamos denominadores y pasamos todo al primer miembro, obtenemos también las ecuaciones implícitas.
Ejercicios
1.Hallar las ecuaciones paramétricas, en forma continua e implícitas de la recta que pasa por el punto A = (1, 2, 1) y cuyo vector director es 
.
.Ecuaciones paramétricas
Ecuaciones en forma continua
Ecuaciones implícitas
miércoles, 10 de abril de 2013
10 de Abril.
El examen de recuperación de la 2ª evaluación se ha aplazado para el martes 16.
Hemos comenzado con un nuevo tema llamado vectores en el espacio, en el que hemos dado:
Operaciones con vectores.
Vector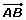
. Origen A extremo B.
Módulo de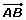 es la distancia de A a B. Se designa así: 
Dirección de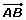 es la recta sobre la que están A y B y la de todas las rectas paralelas a ellas.
Cada dirección admite dos sentidos opuestos de A a B y de B a A.
Dos vectores son iguales cuando tienen el mismo módulo, la misma dirección y el mismo sentido.
Expresión analítica de un vector.
-Dependencia e independencia lineal.
Varios vectores se llaman linealmente dependientes si algunos de ellos se pueden poner como combinación lineal de los demás. Cuando no es así, se llama linealmente independiente.
Por ejemplo.
-Dos vectores alineados son linealmente dependientes.
-Dos vectores no alineados son linealmente independiente.
-Tres vectores coplanarios (están en el mismo plano) son linealmente dependientes, pero tres vectores no coplanarios son independientes.
-Base.
Tres vectores no coplanarios cualesquiera forman una base del espacio vectorial tridimensional.
Si los tres vectores son perpendiculares entre sí, se dice que forman una base ortogonal. Si además tienen la misma longitud (que se toma como unidad), se dice que la base es ortonormal.
Hemos comenzado con un nuevo tema llamado vectores en el espacio, en el que hemos dado:
Operaciones con vectores.
Vector
. Origen A extremo B.Módulo de
es la distancia de A a B. Se designa así: Dirección de
es la recta sobre la que están A y B y la de todas las rectas paralelas a ellas.Cada dirección admite dos sentidos opuestos de A a B y de B a A.
Dos vectores son iguales cuando tienen el mismo módulo, la misma dirección y el mismo sentido.
Expresión analítica de un vector.
-Dependencia e independencia lineal.
Varios vectores se llaman linealmente dependientes si algunos de ellos se pueden poner como combinación lineal de los demás. Cuando no es así, se llama linealmente independiente.
Por ejemplo.
-Dos vectores alineados son linealmente dependientes.
-Dos vectores no alineados son linealmente independiente.
-Tres vectores coplanarios (están en el mismo plano) son linealmente dependientes, pero tres vectores no coplanarios son independientes.
-Base.
Tres vectores no coplanarios cualesquiera forman una base del espacio vectorial tridimensional.
Si los tres vectores son perpendiculares entre sí, se dice que forman una base ortogonal. Si además tienen la misma longitud (que se toma como unidad), se dice que la base es ortonormal.
miércoles, 3 de abril de 2013
3 Abril del 2013.
El examen de recuperación de la segunda evaluación se realizará el día 9 de Abril.
El viernes 22 de Marzo realizamos el examen de Gauss, matrices y determinantes.
En esta semana hemos estado viendo el Teorema de Rouché y Regla de Cramer.
Teorema de Rouché.
Para saber si un sistema de ecuaciones tiene o no solución, habrá que ver si los términos independientes se pueden obtener a partir de los coeficientes de las incógnitas. Esto se realiza comparando la matriz de los coeficientes con la matriz que se obtiene añadiendo a esta la columna de los términos independiente, llamada Matriz ampliada. Es lo que hace el siguiente teorema.
La condición necesaria y suficiente para que tenga solución el sistema es que el rango de la matriz de los coeficiente, A, coincida con el rango de la matriz ampliada, A'.
Es decir: El sistema (*)tiene solución <--> rango(A)=rango(A').
Relación entre ramgo(A) y rango (A') en un sistema incompatible
Si el sistema es incompatible, el ran(A) es distinto a ran(A'). Puesto que A' tiene una columna mas que A, su rango solo puede ser una unidad mayor. Por tanto, si el sistema es incompatible, ran(A')=ran(A)+1.
Regla de Cramer
La regla de Cramer es un teorema con una inmediata utilidad práctica. sirve para obtener la solución de un sistema de n ecuaciones con n incógnitas. Vamos a anunciarlo y demostrarlo para n=4. Su generalización para un n cualquiera es inmediata.
El examen de Gauss, matrices, determinantes con Rouché y Cramer se realizará el viernes 12 de Abril.
El viernes 22 de Marzo realizamos el examen de Gauss, matrices y determinantes.
En esta semana hemos estado viendo el Teorema de Rouché y Regla de Cramer.
Teorema de Rouché.
Para saber si un sistema de ecuaciones tiene o no solución, habrá que ver si los términos independientes se pueden obtener a partir de los coeficientes de las incógnitas. Esto se realiza comparando la matriz de los coeficientes con la matriz que se obtiene añadiendo a esta la columna de los términos independiente, llamada Matriz ampliada. Es lo que hace el siguiente teorema.
La condición necesaria y suficiente para que tenga solución el sistema es que el rango de la matriz de los coeficiente, A, coincida con el rango de la matriz ampliada, A'.
Es decir: El sistema (*)tiene solución <--> rango(A)=rango(A').
Relación entre ramgo(A) y rango (A') en un sistema incompatible
Si el sistema es incompatible, el ran(A) es distinto a ran(A'). Puesto que A' tiene una columna mas que A, su rango solo puede ser una unidad mayor. Por tanto, si el sistema es incompatible, ran(A')=ran(A)+1.
Regla de Cramer
La regla de Cramer es un teorema con una inmediata utilidad práctica. sirve para obtener la solución de un sistema de n ecuaciones con n incógnitas. Vamos a anunciarlo y demostrarlo para n=4. Su generalización para un n cualquiera es inmediata.
El examen de Gauss, matrices, determinantes con Rouché y Cramer se realizará el viernes 12 de Abril.
Suscribirse a:
Entradas (Atom)