En esta semana hemos dado:
Medidas de ángulos entre rectas y planos.
Para el estudio de ángulo entre rectas, entre planos y entre rectas y planos, necesitamos disponer para cada figura de un vector que caracterice su dirección. En la recta. esa papel lo cumple, obviamente, su vector de dirección; en el plano, su vector normal.
-Ángulo entre dos rectas.
-Ángulo entre dos planos.
-Ángulo entre una recta y un plano.
Distancias entre punto, rectas y planos.
-Distancias entre dos puntos.
-Distancia entre un punto y una recta.
-Método constructivo.
-Método del punto genérico.
-Método del producto vectorial: Cálculo directo de la distancia.
-Distancia de un punto a un punto.
-Distancia de una recta a un plano.
-Distancia entre dos planos.
-Distancia entre dos planos.
-Distancias entre dos rectas.
-Método del plano paralelo.
-Método del vector variable
-Método del producto mixto.
Medidas de áreas y de volúmenes.
-Área de un triángulo del que se conocen los vértices.
-Volumen de un tetraedro del que se conocen los vértices.
Lugares geométricos en el espacio.
-Plano mediador.
-Plano bisector.
-Esfera.
-Elipsoides, hiperboloides, paraboloides.
Fin de temario.
Con esto concluimos el curso. Espero que os haya gustado.
miércoles, 15 de mayo de 2013
miércoles, 8 de mayo de 2013
8 de Mayo
Hemos comenzado un nuevo tema, llamado problemas métricos.
En la unidad anterior además de distintas ecuaciones de rectas y planos,hemos visto problemas de paralelismo, intersección e incidencia (¿está un punto en una recta?, ¿está tal recta contenida en un cierto plano?). Todas ellas ---paralelismo, corte e incidencia ---son propiedades afines. Las relaciones en que intervienen medidas (áreas, ángulos, distancias, volúmenes) son propiedades métricas.
En el desarrollo de la geometría métrica, además de las aportaciones de Monge y sus discípulos ( ver la introducción a la unidad anterior), son logros destacables la obtención de la fórmula para hallar la distancia de un punto a un plano (Lagrange) y del volumen de un paralelepípedo (Cauchy).
El español Pedro Puig Adam (1900-1960), gran matemático y extraordinario didacta, fue autor de Geometría Métrica que es un clásico de esta materia.
En el que vemos:
Direcciones entre rectas y planos.
Los problemas afines tratan de incidencias (ver sin punto está contenido en una recta o e un plano y ver si una recta esta contenida en un plano),paralelismos e intersecciones. La perpendicularidad es un problema métrico. Cuando en la unidad anterior utilizamos el vector normal a un plano, o los productos escalares y vectoriales para hallar vectores perpendiculares a otros, estábamos utilizando procedimientos métricos para resolver problemas afines. Vamos a comenzar esta unidad revisando estos procedimientos.
-Dirección de una recta dada en paramétricas.
-Dirección de un plano dada de forma implícita.
-Plano paralelo a dos rectas.
-Rectas definidas por dos planos.
-->Una figura incide en otra cuando esta contenida en ella. (Ten en cuenta que este significado de "incidir" solo se utiliza en geometría).
-->Un figura coincide (co-incide) con otra cuando cada una de ellas incide en la otra.
En la unidad anterior además de distintas ecuaciones de rectas y planos,hemos visto problemas de paralelismo, intersección e incidencia (¿está un punto en una recta?, ¿está tal recta contenida en un cierto plano?). Todas ellas ---paralelismo, corte e incidencia ---son propiedades afines. Las relaciones en que intervienen medidas (áreas, ángulos, distancias, volúmenes) son propiedades métricas.
En el desarrollo de la geometría métrica, además de las aportaciones de Monge y sus discípulos ( ver la introducción a la unidad anterior), son logros destacables la obtención de la fórmula para hallar la distancia de un punto a un plano (Lagrange) y del volumen de un paralelepípedo (Cauchy).
El español Pedro Puig Adam (1900-1960), gran matemático y extraordinario didacta, fue autor de Geometría Métrica que es un clásico de esta materia.
En el que vemos:
Direcciones entre rectas y planos.
Los problemas afines tratan de incidencias (ver sin punto está contenido en una recta o e un plano y ver si una recta esta contenida en un plano),paralelismos e intersecciones. La perpendicularidad es un problema métrico. Cuando en la unidad anterior utilizamos el vector normal a un plano, o los productos escalares y vectoriales para hallar vectores perpendiculares a otros, estábamos utilizando procedimientos métricos para resolver problemas afines. Vamos a comenzar esta unidad revisando estos procedimientos.
-Dirección de una recta dada en paramétricas.
-Dirección de un plano dada de forma implícita.
-Plano paralelo a dos rectas.
-Rectas definidas por dos planos.
-->Una figura incide en otra cuando esta contenida en ella. (Ten en cuenta que este significado de "incidir" solo se utiliza en geometría).
-->Un figura coincide (co-incide) con otra cuando cada una de ellas incide en la otra.
miércoles, 24 de abril de 2013
24 de Abril.
EL día 7 de Mayo se realizará el examen de recuperación de matrices.
En esta semana hemos dados posiciones relativas de dos rectas, puede darse unos de estos casos:
-Coincide misma dirección un punto común.
-Son paralelas misma dirección, ningún punto en común.
-Se cortan distinta dirección, un punto común.
-Se cruzan distinta dirección, ningún punto común.
Hemos de aprender a identificar en cual de los cuatro casos estamos partiendo de las expresiones analítica de la recta, es decir, conociendo sus vectores, posiciones, dirección.
Estudio de las posiciones relativas de rectas mediante rango.
-Las rectas coinciden: ran(M)=ran(M')=1
-Las rectas son paralelas: ran(M)=1, ran(M')=2
-Las rectas se cortan: ran(M)=ran(M')=2
-Las rectas se cruzan: ran(M)=2, ran(M')=3
Posiciones relativas de planos y rectas.
El estudio de las posiciones relativas de planos entre sí y de planos y rectas se reducen en todos sus casos, a la resolución de sistemas de ecuaciones. Si embargo, es conveniente prestar atención especial a algunos de ellos.
Dos planos.
Dos planos pueden cortarse, ser paralelos o coincidir. El sistema formado por sus ecuaciones,,
|ax + by + cz + d = 0
|a'x + b'y + c'z + d' = 0
El estudio de sus rango nos da información sobre sus soluciones (es decir, sobre los puntos comunes a ambos planos) y, por tanto, sobre su posición relativa.
En esta semana hemos dados posiciones relativas de dos rectas, puede darse unos de estos casos:
-Coincide misma dirección un punto común.
-Son paralelas misma dirección, ningún punto en común.
-Se cortan distinta dirección, un punto común.
-Se cruzan distinta dirección, ningún punto común.
Hemos de aprender a identificar en cual de los cuatro casos estamos partiendo de las expresiones analítica de la recta, es decir, conociendo sus vectores, posiciones, dirección.
Estudio de las posiciones relativas de rectas mediante rango.
-Las rectas coinciden: ran(M)=ran(M')=1
-Las rectas son paralelas: ran(M)=1, ran(M')=2
-Las rectas se cortan: ran(M)=ran(M')=2
-Las rectas se cruzan: ran(M)=2, ran(M')=3
Posiciones relativas de planos y rectas.
El estudio de las posiciones relativas de planos entre sí y de planos y rectas se reducen en todos sus casos, a la resolución de sistemas de ecuaciones. Si embargo, es conveniente prestar atención especial a algunos de ellos.
Dos planos.
Dos planos pueden cortarse, ser paralelos o coincidir. El sistema formado por sus ecuaciones,,
|ax + by + cz + d = 0
|a'x + b'y + c'z + d' = 0
El estudio de sus rango nos da información sobre sus soluciones (es decir, sobre los puntos comunes a ambos planos) y, por tanto, sobre su posición relativa.
miércoles, 17 de abril de 2013
17 de Abril.
Hemos empezado nuevo tema llamado "Puntos, rectas y planos en el espacio", que en el examen irá unido al anterior.
Simétrico de un punto respecto de otro.
Si A' es el simétrico de A respecto de M, entonces M es el punto medio del segmento AA'. Por ello se verificará la igualdad.
Ejemplo: Calcula el simétrico de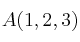
respecto de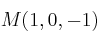 
Llamamos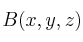
al simétrico buscado. 
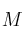será el punto medio del segmento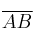 
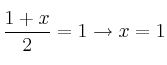
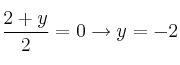
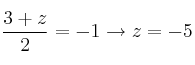
Por tanto, el simétrico es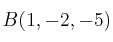
Los ejercicios que hemos realizado en clase son el 1, 2 y 3 pág 156.
Ecuaciones de la recta.
Simétrico de un punto respecto de otro.
Si A' es el simétrico de A respecto de M, entonces M es el punto medio del segmento AA'. Por ello se verificará la igualdad.
Ejemplo: Calcula el simétrico de
respecto de Llamamos
al simétrico buscado. será el punto medio del segmento
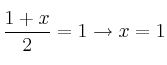
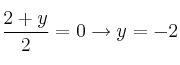
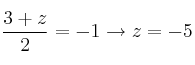
Por tanto, el simétrico es
Los ejercicios que hemos realizado en clase son el 1, 2 y 3 pág 156.
Ecuaciones de la recta.
Ecuación vectorial de la recta
Definimos una recta r como el conjunto de los puntos del espacio, alineados con un punto P y con una dirección dada 
.
.
Si P(x1, y1) es un punto de la recta r, el vector 
tiene igual dirección que , luego es igual a multiplicado por un escalar:
tiene igual dirección que , luego es igual a multiplicado por un escalar:Ecuaciones paramétricas de la recta
Si operamos en la ecuación vectorial de la recta llegamos a la igualdad:
Para que se verifique esta igualdad, se deben cumplir:
Ecuaciones continuas de la recta
Despejando e igualando λ en las ecuaciones paramétricas se tiene:
Ecuaciones implícitas de la recta
Una recta puede venir determinada por la intersección de los planos.
Si en las ecuaciones continuas de la recta quitamos denominadores y pasamos todo al primer miembro, obtenemos también las ecuaciones implícitas.
Ejercicios
1.Hallar las ecuaciones paramétricas, en forma continua e implícitas de la recta que pasa por el punto A = (1, 2, 1) y cuyo vector director es 
.
.Ecuaciones paramétricas
Ecuaciones en forma continua
Ecuaciones implícitas
miércoles, 10 de abril de 2013
10 de Abril.
El examen de recuperación de la 2ª evaluación se ha aplazado para el martes 16.
Hemos comenzado con un nuevo tema llamado vectores en el espacio, en el que hemos dado:
Operaciones con vectores.
Vector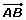
. Origen A extremo B.
Módulo de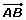 es la distancia de A a B. Se designa así: 
Dirección de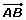 es la recta sobre la que están A y B y la de todas las rectas paralelas a ellas.
Cada dirección admite dos sentidos opuestos de A a B y de B a A.
Dos vectores son iguales cuando tienen el mismo módulo, la misma dirección y el mismo sentido.
Expresión analítica de un vector.
-Dependencia e independencia lineal.
Varios vectores se llaman linealmente dependientes si algunos de ellos se pueden poner como combinación lineal de los demás. Cuando no es así, se llama linealmente independiente.
Por ejemplo.
-Dos vectores alineados son linealmente dependientes.
-Dos vectores no alineados son linealmente independiente.
-Tres vectores coplanarios (están en el mismo plano) son linealmente dependientes, pero tres vectores no coplanarios son independientes.
-Base.
Tres vectores no coplanarios cualesquiera forman una base del espacio vectorial tridimensional.
Si los tres vectores son perpendiculares entre sí, se dice que forman una base ortogonal. Si además tienen la misma longitud (que se toma como unidad), se dice que la base es ortonormal.
Hemos comenzado con un nuevo tema llamado vectores en el espacio, en el que hemos dado:
Operaciones con vectores.
Vector
. Origen A extremo B.Módulo de
es la distancia de A a B. Se designa así: Dirección de
es la recta sobre la que están A y B y la de todas las rectas paralelas a ellas.Cada dirección admite dos sentidos opuestos de A a B y de B a A.
Dos vectores son iguales cuando tienen el mismo módulo, la misma dirección y el mismo sentido.
Expresión analítica de un vector.
-Dependencia e independencia lineal.
Varios vectores se llaman linealmente dependientes si algunos de ellos se pueden poner como combinación lineal de los demás. Cuando no es así, se llama linealmente independiente.
Por ejemplo.
-Dos vectores alineados son linealmente dependientes.
-Dos vectores no alineados son linealmente independiente.
-Tres vectores coplanarios (están en el mismo plano) son linealmente dependientes, pero tres vectores no coplanarios son independientes.
-Base.
Tres vectores no coplanarios cualesquiera forman una base del espacio vectorial tridimensional.
Si los tres vectores son perpendiculares entre sí, se dice que forman una base ortogonal. Si además tienen la misma longitud (que se toma como unidad), se dice que la base es ortonormal.
miércoles, 3 de abril de 2013
3 Abril del 2013.
El examen de recuperación de la segunda evaluación se realizará el día 9 de Abril.
El viernes 22 de Marzo realizamos el examen de Gauss, matrices y determinantes.
En esta semana hemos estado viendo el Teorema de Rouché y Regla de Cramer.
Teorema de Rouché.
Para saber si un sistema de ecuaciones tiene o no solución, habrá que ver si los términos independientes se pueden obtener a partir de los coeficientes de las incógnitas. Esto se realiza comparando la matriz de los coeficientes con la matriz que se obtiene añadiendo a esta la columna de los términos independiente, llamada Matriz ampliada. Es lo que hace el siguiente teorema.
La condición necesaria y suficiente para que tenga solución el sistema es que el rango de la matriz de los coeficiente, A, coincida con el rango de la matriz ampliada, A'.
Es decir: El sistema (*)tiene solución <--> rango(A)=rango(A').
Relación entre ramgo(A) y rango (A') en un sistema incompatible
Si el sistema es incompatible, el ran(A) es distinto a ran(A'). Puesto que A' tiene una columna mas que A, su rango solo puede ser una unidad mayor. Por tanto, si el sistema es incompatible, ran(A')=ran(A)+1.
Regla de Cramer
La regla de Cramer es un teorema con una inmediata utilidad práctica. sirve para obtener la solución de un sistema de n ecuaciones con n incógnitas. Vamos a anunciarlo y demostrarlo para n=4. Su generalización para un n cualquiera es inmediata.
El examen de Gauss, matrices, determinantes con Rouché y Cramer se realizará el viernes 12 de Abril.
El viernes 22 de Marzo realizamos el examen de Gauss, matrices y determinantes.
En esta semana hemos estado viendo el Teorema de Rouché y Regla de Cramer.
Teorema de Rouché.
Para saber si un sistema de ecuaciones tiene o no solución, habrá que ver si los términos independientes se pueden obtener a partir de los coeficientes de las incógnitas. Esto se realiza comparando la matriz de los coeficientes con la matriz que se obtiene añadiendo a esta la columna de los términos independiente, llamada Matriz ampliada. Es lo que hace el siguiente teorema.
La condición necesaria y suficiente para que tenga solución el sistema es que el rango de la matriz de los coeficiente, A, coincida con el rango de la matriz ampliada, A'.
Es decir: El sistema (*)tiene solución <--> rango(A)=rango(A').
Relación entre ramgo(A) y rango (A') en un sistema incompatible
Si el sistema es incompatible, el ran(A) es distinto a ran(A'). Puesto que A' tiene una columna mas que A, su rango solo puede ser una unidad mayor. Por tanto, si el sistema es incompatible, ran(A')=ran(A)+1.
Regla de Cramer
La regla de Cramer es un teorema con una inmediata utilidad práctica. sirve para obtener la solución de un sistema de n ecuaciones con n incógnitas. Vamos a anunciarlo y demostrarlo para n=4. Su generalización para un n cualquiera es inmediata.
El examen de Gauss, matrices, determinantes con Rouché y Cramer se realizará el viernes 12 de Abril.
miércoles, 13 de marzo de 2013
13 de Marzo.
En esta semana hemos dado un nuevo tema llamado determinantes. En el que hemos dado determinantes de orden 2, determinantes de orden 3, determinantes de orden cualquiera, menor complementario y adjunto, desarrollo de un determinante por los elementos de una línea, método para calcular determinantes de orden cualquiera y el rango de una matriz a partir de sus menores.
En el cual hemos realizado relaciones de ejercicios.
El examen se realizará el día viernes 22 de Marzo.
En el cual hemos realizado relaciones de ejercicios.
El examen se realizará el día viernes 22 de Marzo.
6 de Marzo
En el tema de álgebra de matrices hemos dado:
-Nomenclatura. Definiciones.
Ejercicios 1, 2 y 3 pág 51
-Operaciones con matrices
Ejercicio 1 pág 52 y 2 y 3 pág 55.
-Propiedades de las operaciones con matrices.
Ejercicios 1 y 2 pág 57
-Matrices cuadradas.
Ejercicios 1 y 2 pág 59 y 3, 4, 6, 8, 9 y 10 pág 61
-Complementos teóricos para el estudio de matrices.
Ejercicios 1 pág 62 y 2, 3, 4 y 5 pá 64.
-Rango de una matriz.
Ejercicio 1 pág 66 y 4, 6, 8, 10 y 13 pág 72.
-Nomenclatura. Definiciones.
Ejercicios 1, 2 y 3 pág 51
-Operaciones con matrices
Ejercicio 1 pág 52 y 2 y 3 pág 55.
-Propiedades de las operaciones con matrices.
Ejercicios 1 y 2 pág 57
-Matrices cuadradas.
Ejercicios 1 y 2 pág 59 y 3, 4, 6, 8, 9 y 10 pág 61
-Complementos teóricos para el estudio de matrices.
Ejercicios 1 pág 62 y 2, 3, 4 y 5 pá 64.
-Rango de una matriz.
Ejercicio 1 pág 66 y 4, 6, 8, 10 y 13 pág 72.
27 de Febrero.
En esta semana hemos realizado una relación de ejercicios de sistemas de ecuaciones.
1. Un cajero automático contiene sólo billetes de 10, 20 y 50 euros. En total hay 130 billetes con un importe de 3000 euros
a) ¿Es posible que en el cajero haya el triple número de billetes de 10 que de 50?
b) Suponiendo que el número de billetes de 10 es el doble que el de 50, calcula cuántos billetes hay de cada tipo.
2. Un autobús transporta en cierto viaje 60 viajeros de tres tipos: los que pagan el billete entero que vale 1 euro, estudiantes que tienen un 25% de descuento; y jubilados que pagan sólo el 50%. La recaudación de este viaje fue 48 €, calcula el número de viajero de cada clase sabiendo que el número de estudiantes era el doble que el resto de viajero.
3. Un trayecto de 200 Km se ha de hacer combinando taxi, ferrocarril y autobús. El coste del taxi es de 5 €/Km, el del ferrocarril es de 2 €/Km y el del autobús 3€/Km el recorrido nos ha costado 500 € pues hemos hecho el doble de Km en ferrocarril que taxi y autobús juntos determina las distancias que hemos recorrido en cada medio de transporte.
4.En una fabrica de artículos deportivos se dispone de 10 cajas de diferentes tamaños: para 50, 30 y 25 camisetas, respectivamente si una caja grande fuera mediana, entonces habría el mismo número de grandes que de medianas en total de envasan 390 camisetas. Determina el número de cajas que hay de cada clase final-
5. El cajero de un banco sólo dispone de billetes de 10, 20 y 50. Hemos sacado 290 € en 8 billetes. El número de billetes de 10€ es el doble que e de 20 € plantea y resuelve el sistema de ecuaciones que se tiene que usar para saber cuantos billetes de cada clase hemos sacado.
En esta semana empezaremos con un nuevo tema el álgebra de matrices.
1. Un cajero automático contiene sólo billetes de 10, 20 y 50 euros. En total hay 130 billetes con un importe de 3000 euros
a) ¿Es posible que en el cajero haya el triple número de billetes de 10 que de 50?
b) Suponiendo que el número de billetes de 10 es el doble que el de 50, calcula cuántos billetes hay de cada tipo.
2. Un autobús transporta en cierto viaje 60 viajeros de tres tipos: los que pagan el billete entero que vale 1 euro, estudiantes que tienen un 25% de descuento; y jubilados que pagan sólo el 50%. La recaudación de este viaje fue 48 €, calcula el número de viajero de cada clase sabiendo que el número de estudiantes era el doble que el resto de viajero.
3. Un trayecto de 200 Km se ha de hacer combinando taxi, ferrocarril y autobús. El coste del taxi es de 5 €/Km, el del ferrocarril es de 2 €/Km y el del autobús 3€/Km el recorrido nos ha costado 500 € pues hemos hecho el doble de Km en ferrocarril que taxi y autobús juntos determina las distancias que hemos recorrido en cada medio de transporte.
4.En una fabrica de artículos deportivos se dispone de 10 cajas de diferentes tamaños: para 50, 30 y 25 camisetas, respectivamente si una caja grande fuera mediana, entonces habría el mismo número de grandes que de medianas en total de envasan 390 camisetas. Determina el número de cajas que hay de cada clase final-
5. El cajero de un banco sólo dispone de billetes de 10, 20 y 50. Hemos sacado 290 € en 8 billetes. El número de billetes de 10€ es el doble que e de 20 € plantea y resuelve el sistema de ecuaciones que se tiene que usar para saber cuantos billetes de cada clase hemos sacado.
En esta semana empezaremos con un nuevo tema el álgebra de matrices.
20 de Febrero
En esta semana seguimos repasando el tema de método de Gauss.
Hemos realizado estos ejercicios.
-1 y 2 pág 33
-1 y 2 pág 34
-1 pág 35
-1 y 2 pág 38
-1 y 2 pág 39
-17 b, 20 a,b y 25 pág 45
Hemos realizado estos ejercicios.
-1 y 2 pág 33
-1 y 2 pág 34
-1 pág 35
-1 y 2 pág 38
-1 y 2 pág 39
-17 b, 20 a,b y 25 pág 45
miércoles, 6 de marzo de 2013
13 de Febrero
En esta semana hemos comenzado un nuevo tema llamado sistema de ecuaciones. Método de gauss.
En este tema hemos dado:
- La ecuación lineal es una ecuación polinómica de grado uno o con varias incógnitas.
-Ecuaciones equivalentes, dos ecuaciones son equivalentes cuando tienen la misma solución (o las mismas soluciones).
-Sistema de ecuaciones lineales, varias ecuaciones dadas conjuntamente con el fin de determinar la solución o las soluciones comunes a todas ellas forman un sistema de ecuaciones.
-Sistemas equivalentes, dos sistemas de ecuaciones son equivalentes si tienen la misma soluciones. Dos sistemas pueden ser equivalentes sin que lo sean las ecuaciones que los forman.
-Trasformaciones en un sistema de ecuaciones, se llaman transformaciones válidas a las que mantienen la soluciones del sistema.
-Sistemas de ecuaciones con dos incógnitas.
-Sistemas de ecuaciones con tres incógnitas.
-MÉTODO DE GAUSS, el método de Gauss consiste en transformar un sistema de ecuaciones lineales en otro escalonado. Para ello, "hacemos cero" sometiendo las ecuaciones a dos transformaciones elementales:
-Multiplicar una ecuación por un número distinto de cero.
-Sumar a una ecuación otra multiplicada por un número.
En este tema hemos dado:
- La ecuación lineal es una ecuación polinómica de grado uno o con varias incógnitas.
-Ecuaciones equivalentes, dos ecuaciones son equivalentes cuando tienen la misma solución (o las mismas soluciones).
-Sistema de ecuaciones lineales, varias ecuaciones dadas conjuntamente con el fin de determinar la solución o las soluciones comunes a todas ellas forman un sistema de ecuaciones.
-Sistemas equivalentes, dos sistemas de ecuaciones son equivalentes si tienen la misma soluciones. Dos sistemas pueden ser equivalentes sin que lo sean las ecuaciones que los forman.
-Trasformaciones en un sistema de ecuaciones, se llaman transformaciones válidas a las que mantienen la soluciones del sistema.
-Sistemas de ecuaciones con dos incógnitas.
-Sistemas de ecuaciones con tres incógnitas.
-MÉTODO DE GAUSS, el método de Gauss consiste en transformar un sistema de ecuaciones lineales en otro escalonado. Para ello, "hacemos cero" sometiendo las ecuaciones a dos transformaciones elementales:
-Multiplicar una ecuación por un número distinto de cero.
-Sumar a una ecuación otra multiplicada por un número.
viernes, 1 de marzo de 2013
6 de Febrero.
En esta semana hemos estado repasando cálculo de áreas, puesto que el examen se realizará el viernes.
Aquí dejamos unos ejercicios para repasar.
Aquí dejamos unos ejercicios para repasar.
30 de Enero
Esta semana realizaremos el examen de cálculos de integrales.
Aquí dejamos algunas integrales con sus soluciones para repasar.
Aquí dejamos algunas integrales con sus soluciones para repasar.
miércoles, 23 de enero de 2013
23 de Enero.
En esta semana hemos realizado el examen de recuperación.
Hemos realizado ejercicios bastante interesantes de cálculo de áreas de integrales:
pág 381 ej 4, 5, 9 a y b, 10 a, b, c, e, 12, 13.
pág 382 ej 21, 25.
pág 383 ej 36 y 37.
Aquí dejamos la tabla de integrales.
Todavía no hemos fijado la fecha del examen de integrales pero posiblemente sea la próxima semana.
Hemos realizado ejercicios bastante interesantes de cálculo de áreas de integrales:
pág 381 ej 4, 5, 9 a y b, 10 a, b, c, e, 12, 13.
pág 382 ej 21, 25.
pág 383 ej 36 y 37.
Aquí dejamos la tabla de integrales.
Todavía no hemos fijado la fecha del examen de integrales pero posiblemente sea la próxima semana.
miércoles, 16 de enero de 2013
16 de Enero.
En esta semana hemos empezado un tema nuevo, aplicaciones de las integrales en el que hemos visto el calculo de áreas.
Hay infinidad de funciones extraídas del mundo real (científico, económico...) para las cuales tienes especial relevancias el área bajo su gráfica. Vamos a ocuparnos del calculo de esas áreas.
Nos vamos a centrar en el cálculo de área bajo una función continua porque, en este nivel, todas las funciones que manejamos, o bien son continuas, o bien están formadas por trozos de de funciones continuas.
Hemos realizado los ejercicios:
- 1 y 2 de la pág 374.
*La recuperación del primer trimestre esta fijada para el 22 de Enero a las 18:00 de la tarde, duración aproximada de dos horas.
Hay infinidad de funciones extraídas del mundo real (científico, económico...) para las cuales tienes especial relevancias el área bajo su gráfica. Vamos a ocuparnos del calculo de esas áreas.
Nos vamos a centrar en el cálculo de área bajo una función continua porque, en este nivel, todas las funciones que manejamos, o bien son continuas, o bien están formadas por trozos de de funciones continuas.
Hemos realizado los ejercicios:
- 1 y 2 de la pág 374.
*La recuperación del primer trimestre esta fijada para el 22 de Enero a las 18:00 de la tarde, duración aproximada de dos horas.
miércoles, 9 de enero de 2013
9 de Enero.
Hemos repasado integrales primitivas y integración "por partes", hemos visto una nueva forma de integración, integración de funciones racionales.
Nos ha mandado una relación de ejercicios en el que te explica formas de hacer la integrales.
-Como ya hemos visto, en muchas ocasiones los cambios de variable se pueden hacer "de cabeza" (no es necesario usar otra letra t); eso ocurre cuando la función cuya primitiva buscamos "esconde muy poco" una integral inmediata. No ocurre así con otras funciones y, en estos casos, el cambio es imprescindible. No hay normas fijas, pero muchas funciones con raíces exigen cambios explícitos.
-Las funciones trigonométricas se pueden integrar en ocasiones de formas mucho mas cómoda si se utilizan formas adecuadas.
"
Nos ha mandado una relación de ejercicios en el que te explica formas de hacer la integrales.
-Como ya hemos visto, en muchas ocasiones los cambios de variable se pueden hacer "de cabeza" (no es necesario usar otra letra t); eso ocurre cuando la función cuya primitiva buscamos "esconde muy poco" una integral inmediata. No ocurre así con otras funciones y, en estos casos, el cambio es imprescindible. No hay normas fijas, pero muchas funciones con raíces exigen cambios explícitos.
-Las funciones trigonométricas se pueden integrar en ocasiones de formas mucho mas cómoda si se utilizan formas adecuadas.
"
Suscribirse a:
Entradas (Atom)